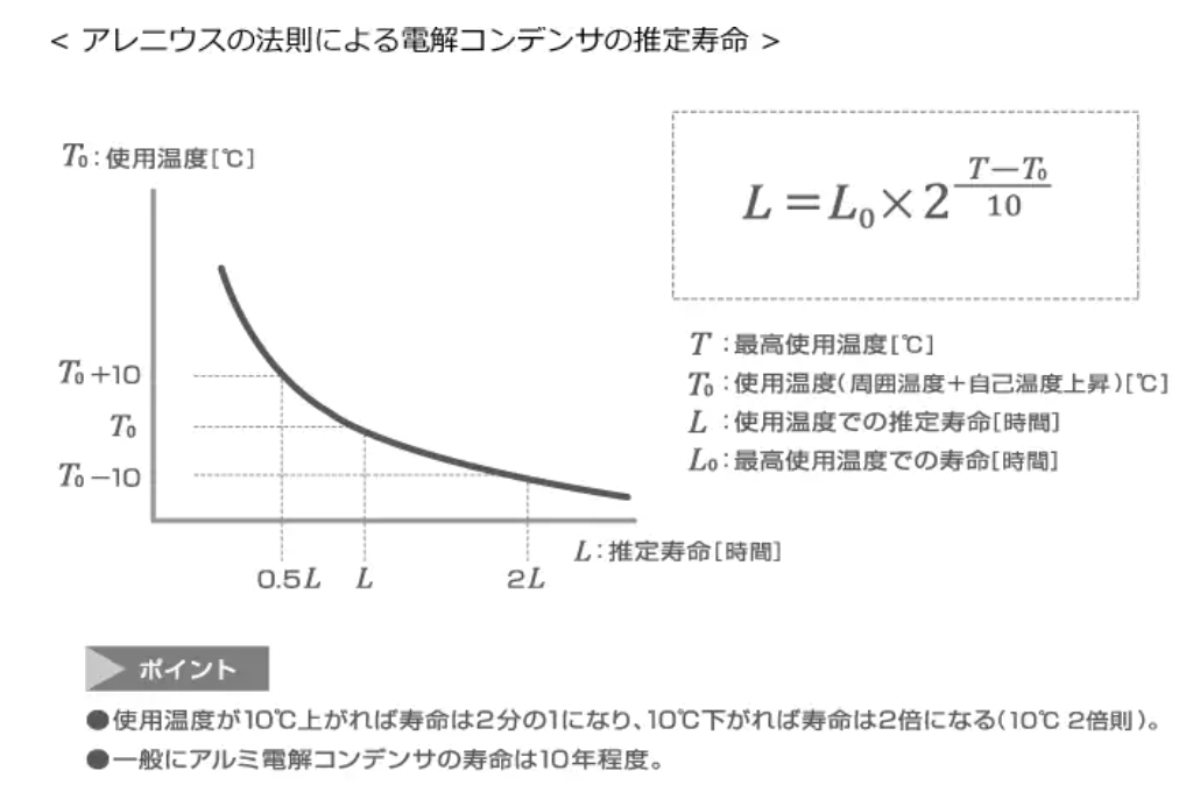
Arrhenius’s 10℃ rule
The life of the electrolytic capacitor is calculated by “Arrhenius’s 10 ° C rule”. A formula published by Swedish scientist Svante Arrhenius in 1884 to predict the rate of a chemical reaction at a certain temperature. To put it simply, the 10 ° C double rule is an empirical rule that “when the temperature rises or falls by 10 ° C, the speed and life of the material deteriorates by double or half.”
‘T’ is the maximum operating temperature of the electrolytic capacitor. Today, industrial power supplies are 105℃, but previously they were 85℃ products. Naturally, an electrolytic capacitor at 105℃ is more resistant to use at high temperatures.
L₀ is the life of the electrolytic capacitor itself. The electrolytic capacitor manufacturer sets a warranty time for each product. For example, if “105 ° C for 5,000 hours”, L₀ is 5,000. This means that the performance is guaranteed for 5,000 hours when used at the maximum operating temperature of 105 ° C for electrolytic capacitors. The operating temperature is the surface temperature of the electrolytic capacitor, usually the surface temperature of the explosion-proof valve of the electrolytic capacitor.
If an electrolytic capacitor with “105℃ for 5,000 hours” is operated for 24 hours, it will only last for half a year in calculation. It is the life when the electrolytic capacitor is used at the maximum operating temperature of 105℃. It takes 1 year at 95℃, 2 years at 85℃, and 4 years at 75℃. Therefore, how to lower the surface temperature of electrolytic capacitors is a showcase for power supply manufacturers.
When I try to calculate using Arrhenius’s 10 ℃ law
I understand Arrhenius’s law, but it is a little difficult to calculate by actually substituting numerical values. Let’s actually calculate the expected life when the maximum operating temperature of the electrolytic capacitor is 105℃ and the guaranteed L₀ = 5,000h.
- When the operating temperature of the electrolytic capacitor is MAX 105 ℃
Since T-T₀ = 105-105 = 0, L = 5000 × 2 0⁄10 = 5000 × 2⁰ = 5,000h 2⁰ = 1, so 5000 × 1 = 5000h
Of course, the guaranteed value is 5,000 hours. - When the specified temperature of the electrolytic capacitor is 95 ° C
Since T-T₀ = 105-95 = 10, L = 5000 × 2 10⁄10 = 5000 × 2¹ = 5000 × 2 = 10,000h
When the surface temperature of the electric controller was lowered by 10 ° C, it doubled to 10,000 hours. - When the specified temperature of the electrolytic capacitor is 85 ° C
Since T-T₀ = 105-85 = 20, L = 5000 × 2 20⁄10 = 5000 × 2² = 5000 × 4 = 20,000h
When the surface temperature of the electric controller was lowered by 20 ° C, it was quadrupled to 20,000 hours. - When the specified temperature of the electrolytic capacitor is 75 ° C
Since T-T₀ = 105-75 = 30, L = 5000 × 2 30⁄10 = 5000 × 2³ = 5000 × 8 = 40,000h
When the surface temperature of the electric controller was lowered by 30 ° C, it increased eight times to 40,000 hours.
The above is easy to calculate with positive integral powers of 2, but let’s calculate with a fraction that is not an integer.
- When the specified temperature of the electrolytic capacitor is 70 ℃
Since T-T₀ = 105-70 = 35, L = 5000 × 2 35⁄10 = 5000 × 2 7⁄2.
2 7⁄2 = (2⁷) ½ = √2⁷. This is such a rule, so I have to remember it. I think it’s at the number III level.
5000 × (2⁷) ½ = 5000 × √2⁷ = 5000 × √128 = 5000 × 11.3 = 56568h
It will be about 56,000 hours.